LOAM论文与代码阅读（一）激光里程计

LOAM 是LiDAR SLAM早期的奠基之作，后续的LeGO-LOAM, lio-sam，ALOAM等方法都以这种高频里程计，低频建图为基础框架。我在最初接触SLAM时学习过这一系列算法，但理解的不深，后来因为没有做lidar SLAM相关，很久不接触已经生疏了。近期考虑到面试需求和未来的职业方向，计划重新学一遍，同时把重点记录下来，以便后续回顾。

LOAM的基本流程如下：

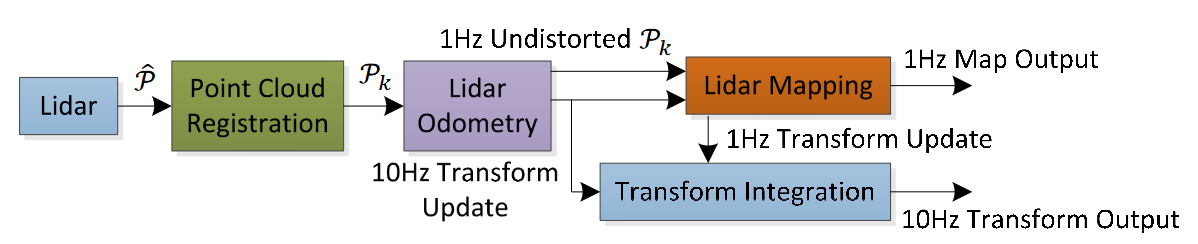
每一帧lidar通过特征提取，运动补偿，特征匹配得到帧与帧之间的位姿（高频）。将几帧拼在一起与地图进行匹配，优化这几帧相对于地图的位姿（低频）。

硬件

这里发现之前忽略的一个点。LOAM中使用的激光雷达与现在的多线机械式激光雷达（如velodyne-32）不同。作者是用一个单线激光雷达加上垂直旋转的电机实现3维的扫描。

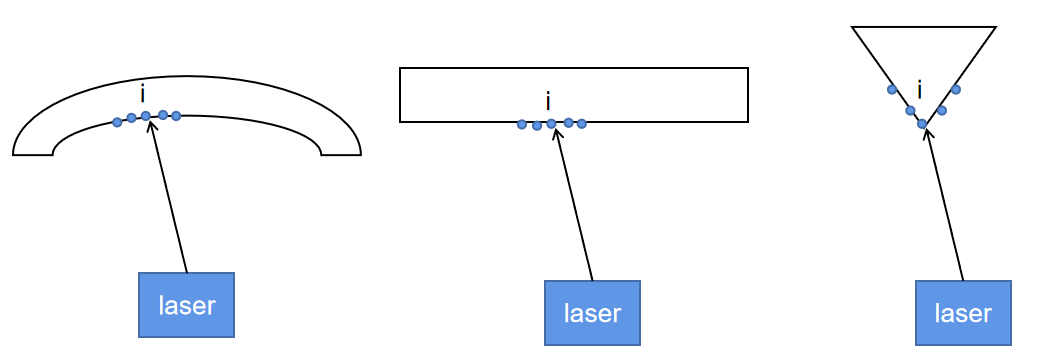
论文中的介绍如上图所示，我的理解是：

单线激光雷达自身水平旋转，水平视场角为180度，分辨率为0.25度。每次旋转180得到的数据称为一个scan，需要25ms。同时电机使得激光雷达整体在垂直方向上旋转，从-90到90，水平为0（因此垂直视场角是180）。这样垂直转180度需要1s，1s内得到的数据是一个sweep。这一秒内会扫描40个scan。相当于在垂直方向上是40线,角分辨率是4.5度。

这也解释了这里scan的指代和其他论文不对应的问题。当前较多使用的多线激光雷达，可近似认为垂直方向的多条laser是同时发射的（实际上不同时，但相隔时间非常接近），因此把多线在水平方向一个周期内的扫描称为一个scan，用于特征提取。

特征提取

如上所述，由于垂直角分辨率是4.5度，角度较大，因此提取特征是对每个scan进行单独操作。希望提取的特征点是边缘（edge）和平面（planar surface）上的点。

边缘和平面特征显著，容易提取，反应了环境的结构，在帧与帧之间保持不变，更有利于匹配。

为了提取边缘点和平面点，我们首先要计算每个点的曲率。一个scan是单线激光按顺时针或逆时针扫描得到的点，如下图所示，为计算点i的曲率，我们取它前后N个点，组成集合S。

则曲率c为：

\[c= \frac{1}{|S| \cdot \|X_ {(k,i)|} \|}\| \sum_{j \in S,j \neq i} ( X_ {(k,i)}^ {L} - X_{(k,j)}^ {L} ) \| \]

\(X_{(k,i)}^L\)是第k个sweep中第i个点在LiDAR坐标系下的坐标。对集合中的每个点计算其与相邻点的距离，用来近似这个点所在位置的曲率。可以想象在平面处相邻点的距离比较接近，曲率会较小，而边缘处点的距离会较远，曲率较大。

对应ALOAM中的代码

// 取每个点前后5个点，算x,y,z方向的差
for (int i = 5; i < cloudSize - 5; i++)
{ 
    float diffX = laserCloud->points[i - 5].x + laserCloud->points[i - 4].x + laserCloud->points[i - 3].x + laserCloud->points[i - 2].x + laserCloud->points[i - 1].x - 10 * laserCloud->points[i].x + laserCloud->points[i + 1].x + laserCloud->points[i + 2].x + laserCloud->points[i + 3].x + laserCloud->points[i + 4].x + laserCloud->points[i + 5].x;
    float diffY = laserCloud->points[i - 5].y + laserCloud->points[i - 4].y + laserCloud->points[i - 3].y + laserCloud->points[i - 2].y + laserCloud->points[i - 1].y - 10 * laserCloud->points[i].y + laserCloud->points[i + 1].y + laserCloud->points[i + 2].y + laserCloud->points[i + 3].y + laserCloud->points[i + 4].y + laserCloud->points[i + 5].y;
    float diffZ = laserCloud->points[i - 5].z + laserCloud->points[i - 4].z + laserCloud->points[i - 3].z + laserCloud->points[i - 2].z + laserCloud->points[i - 1].z - 10 * laserCloud->points[i].z + laserCloud->points[i + 1].z + laserCloud->points[i + 2].z + laserCloud->points[i + 3].z + laserCloud->points[i + 4].z + laserCloud->points[i + 5].z;

    cloudCurvature[i] = diffX * diffX + diffY * diffY + diffZ * diffZ;
    cloudSortInd[i] = i;
    cloudNeighborPicked[i] = 0;
    cloudLabel[i] = 0;
}

对一个scan的曲率按照c值排序，其中最大的n个点选择为edge点，最小的m个点为平面点。为了使得特征点分布更均匀，论文把一个scan平分为4个子区域，每个子区域最多选2个边缘点，4个平面点，边缘和平面有设定一个阈值（只有超过阈值才可能选为边缘点）。

此外，还要去掉一些不可信赖的点： (1) 附近已经有点选中了（避免特征点太集中） (2) 局部平面和laser光束平行，如下图（a） (3) 在被遮挡的区域边缘的点，如下图（b）

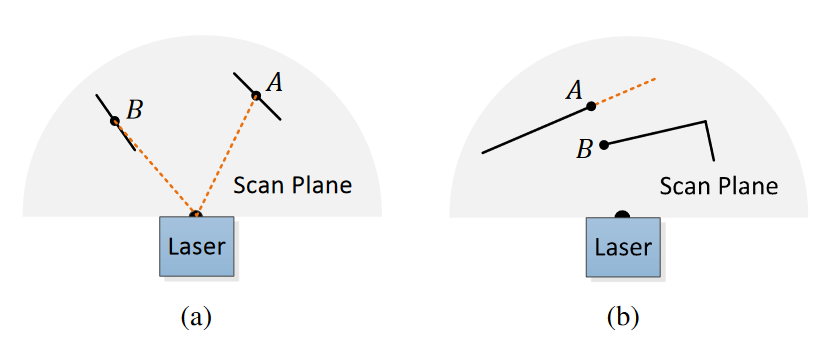
这些点的删除方式是：当根据曲率得到特征点后，重新去看这些点用于计算曲率的点集S，需要保证S中的点没有被选中为特征点，点集构成的平面不与激光线平行，且点集中相邻点没有在激光方向上的出现距离的不连续。

特征匹配

符号

第k个sweep的原始点云表示为\(P_k\)，\(P_k\)开始的时间为\(t_k\)。经过运动补偿（统一到这一帧结束时刻）的点云为\(\overline{P}_k\)。

整体流程

为了对流程有整体的认知，明白每一步的原因，我们先看大致的lidar odometry的流程，细节留到后面分析：

• 输入：前一帧去畸变的点云\(\overline{P}_k\)，当前帧不断增加的点云\(P_k\)（由于程序是实时运行的），

• 输出：\(T^L_{k+1}\),是lidar在\((t_{k+1}\)，\(t_{k+2})\)之间的变换，即点云 \(\overline{P}_{k+1}\) 相对于 \(\overline{P}_{k}\) 变换

\(T^L_{k+1}\)是通过不断迭代获得的。在k+1帧起始时刻\(t_{k+1}\)，\(T^L_{k+1}\)为单位矩阵。我们现在假设上一次迭代得到的位姿为\(T^{L}_{k+1}\)，来推导一次迭代过程：

1. 特征提取：首先从\(P_{k+1}\)中提取edge和plane特征点，用\(\varepsilon_{k+1},H_{k+1}\)表示。
2. 运动补偿：为了和上一帧做匹配，我们可以用\(T^L_{k+1}\)和匀速运动模型将\(\varepsilon_{k+1}, H_{k+1}\)投影到这一帧开始时刻，表示为\(\widetilde{\varepsilon}_{k+1},\widetilde{H}_{k+1}\)（细节1）。
3. 特征匹配：将\(\widetilde{\varepsilon}_{k+1},\widetilde{H}_{k+1}\)与上一帧\(\overline{P}_k\)匹配。对边缘点，我们找到上一帧对应的线，计算点到线的距离。对平面点，我们找到上一帧对应的平面，计算点到平面的距离。（细节2）。
4. 位姿优化：这些距离是\(T^L_{k+1}\)的一个非线性函数，每个距离根据特征点会分配一个权重。构成了对T一个非线性优化问题，应用LM优化求解。将上一次的\(T^L_{k+1}\)作为初值，当迭代一定次数或者函数收敛后，返回新的\(T^L_{k+1}\)。（细节3）。

这个迭代在sweep内不停地进行，直到sweep结束，并把\(P_{k+1}\)所有点用\(T^L_{k+1}\)投影到这一帧结束（运动补偿），得到\(\overline{P}_{k+1}\)作为下一帧的输入。

接下来我们看这里面每一步的细节：

细节1：运动补偿

由于机械式lidar所有点获得的时间戳不同，在lidar运动时，每个点的lidar坐标系实际位置不同。我们要对一个sweep的lidar做运动补偿，把所有(x,y,z)的坐标系统一到一个时刻，作为一帧点云。原始的LOAM没有用IMU，而是假设在一个sweep内角速度和线速度是恒定的。整个过程中涉及运动补偿的流程有两个，一是为了与上一帧进行特征匹配，把所有点投影到这一帧开始时刻，二是在迭代结束之后，把所有点投影到这一帧结束时刻作为下一帧输入。

把\(P_{k+1}\)的点投影到开始时刻： 为了把各个时刻的点投影到这一帧开始，我们需要知道每个点相对于这一帧初始时刻的位姿，这个位姿可以通过对\(T^L_{k+1}\)插值得到。\(T^L_{k+1}\)是当前时刻t下，我们估计的\((t_{k+1}, t)\)变化的位姿。

对于i时刻的点，我们求得的位姿变换如下：

\[ T_{(k+1,i)}^{L} = \frac{t_{i}-t_{k+1}}{t-t_{k+1}} T_{k+1}^ {L} \]

从\(T_{(k+1,i)}^{L}\)中拆解出R,t，可以得到补偿后的特征点坐标\(\widetilde {X}_ {(k+1,i)}^L\)

\[ X_{(k+1,i)}^L =R \widetilde {X}_ {(k+1,i)}^L + t \]

把\(P_{k+1}\)的点投影到结束时刻：

在这一帧结束后，我们得到了\((t_{k+1}\)，\(t_{k+2})\)之间的位姿变换\(T_{k+1}^{L}\)。我们先把所有点按照上述方法投影到这一帧的开始时刻，然后用\(T_{k+1}^{L}\)反变换，将所有点投影到这一帧结束时刻。

对应ALOAM的代码：

//（TransformToStart：将当前帧Lidar坐标系下的点云变换到这一帧开始
void TransformToStart(PointType const *const pi, PointType *const po)
{
    //interpolation ratio
    double s;            //插值比，根据时间，在这一帧里占的比率
    if (DISTORTION)      //是否需要去畸变
    // intensity 实数部分存的是scan上点的id，小数部分存的这一点相对这一帧起始点的时间差
    // intensity的整体减去整数部分,就是时间差,除以周期,就是时间占比了
        s = (pi->intensity - int(pi->intensity)) / SCAN_PERIOD;
    else
        s = 1.0;

    // 所有点的操作方式都是一致的，相当于从结束时刻补偿到起始时刻，相当于是一个匀速模型的假设

    Eigen::Quaterniond q_point_last = Eigen::Quaterniond::Identity().slerp(s, q_last_curr); //slerp函数(球面线性插值)
    Eigen::Vector3d t_point_last = s * t_last_curr;
    Eigen::Vector3d point(pi->x, pi->y, pi->z);         //把当前点的坐标取出
    Eigen::Vector3d un_point = q_point_last * point + t_point_last; //通过旋转和平移将 当前点转到帧起始时刻坐标系下的坐标

    //将求得的转换后的坐标赋值给输出点
    po->x = un_point.x();
    po->y = un_point.y();
    po->z = un_point.z();
    po->intensity = pi->intensity;
}


// 首先把点统一到起始时刻坐标系下,再通过反变换,得到结束时刻坐标系下的点
void TransformToEnd(PointType const *const pi, PointType *const po)
{
    // undistort point first
    pcl::PointXYZI un_point_tmp;
    TransformToStart(pi, &un_point_tmp);        //转到帧起始时刻坐标系下的点

    Eigen::Vector3d un_point(un_point_tmp.x, un_point_tmp.y, un_point_tmp.z);       //取出起始时刻坐标系下的点的x,y,z
    Eigen::Vector3d point_end = q_last_curr.inverse() * (un_point - t_last_curr);   //通过反变换,求得转到 结束时刻坐标系下 的点坐标

    //将求得的转换后的坐标赋值给输出点
    po->x = point_end.x();
    po->y = point_end.y();
    po->z = point_end.z();

    //Remove distortion time info  去完畸变可以删除每个点的时间信息
    po->intensity = int(pi->intensity);
}

细节2：特征匹配

用\(\widetilde{\varepsilon}_{k+1}, \widetilde{H}_{k+1}\)表示投影到开始时刻的特征点。特征匹配的方式如下：

边缘点（图a)：

对于\(\widetilde{\varepsilon}_{k+1}\)中的点i，我们要找到它在k帧中对应的边缘线，为了确定这条线，我们需要找到两个点。一个点j为离i距离最近的点。一个点l是在点j所在scan（橙线）的相邻两个scan（蓝线）中找到离i最近的点。为了确认j,l是边缘点，会确认它们的曲率c（根据特征提取时的公式）。

原因：因为一条边缘线不可能包含一个scan内的多个点。如果这条边缘线由一个scan内的两个点组成，那么这个边缘线与scan所在平面平行，此时这条边缘线在这个scan中的点是一条直线，不会计算出高的曲率，因此不可能被提取为特征点。

得到j,l后，我们计算点到直线的距离来衡量匹配的程度：

\[ d_\varepsilon = \frac{|(\widetilde{X}^L_{(k+1,i)}-\overline{X}^L_{(k,j)})\times (\widetilde{X}^L_{(k+1,i)}-\overline {X}^L_{(k,l)})|}{|\overline{X}^L_{(k,j)}-\overline{X}^L_{(k,l)}|} \]

平面点（图b):

对于\(\overline{H}_{k+1}\)中的点 \(i\)，我们要找到它在k帧中对应的平面，为了确定这个平面，我们需要找到三个点。同样，一个点j为离i距离最近的点。然后我们找到另外两个距离i最近的点\(l,m\)。其中\(l\)需要与点\(j\)在同一个scan（橙线），点\(m\)在相邻两个scan（蓝线）。为了确认j,l是平面点，会确认它们的曲率c

原因：为了防止三点共线？

得到j,l,m后，我们计算点到平面的距离来衡量匹配的程度：

\[ d_H = \frac{\left| \begin{matrix} (\widetilde{X}^L_{(k+1,i)}-\overline{X}^L_{(k,j)}) \\ ((\overline{X}^L_{(k,j)}-\overline{X}^L_{(k,l)})\times (\overline{X}^L_{(k,l)}-\overline {X}^L_{(k,m)})) \end{matrix} \right| }{|(\overline{X}^L_{(k,j)}-\overline{X}^L_{(k,l)})\times (\overline{X}^L_{(k,l)}-\overline {X}^L_{(k,m)})|} \]

为了更快找最近邻，\(\overline{P}_k\)是以3D kd-tree存储的

位姿优化

对于边缘点，我们可以得到损失函数：

\[ f _\varepsilon ( X_ {(k+1,i)}^ {L} , T_ {k+1}^ {L} )=d_\varepsilon ,i \in \varepsilon_ {k+1} \]

对于平面点，我们可以得到损失函数：

\[ f_H ( X_{(k+1,i)}^ {L} , T_ {k+1}^ {L} )=d_H ,i \in H_ {k+1} \]

把这些损失放在一起，可以得到：

\[ \textbf{f}(T_{k+1}^L) = \textbf{d} \]

其中 \(\textbf{d}\) 的每一行都是一个特征点的损失。我们可以计算f相对于T的雅可比矩阵J，然后用LM算法来优化。在优化时每行损失分配了不同的权重，匹配距离大的点权重更小，匹配距离大于一定值的点权重为0（被认为是误匹配）。也就是Bisquare weights, 根据每一项损失当前的大小分配权重，优先去降低小的损失项，减轻大的损失项的影响。这种方式更加鲁棒。

这部分在代码中是用ceres来实现的，每一个残差项通过AddResidualBlock加入损失函数，调用优化器求解。